
However, there are so many external factors that can influence the speed of sound, like small temperature variations, the reaction time of the stopwatch, pressure changes in the laboratory, wind velocity changes, and other random errors. By taking the mean of these values, we can get the average speed of sound in this medium. Hope now you cleared with Standard Error of the Mean in R.As an example, consider an experiment that measures the speed of sound in a material along the three directions (along x, y and z coordinates). As a result, the two datasets have the same mean, but the second dataset has a higher sample size, therefore the standard error is reduced. The first dataset is simply repeated twice in the second dataset. Let’s duplicate the same set of values then see the SEM. When compared to the previous dataset, this indicates that the values in this dataset are more spread out around the mean.Ĭonsider the standard error of the mean for the following two datasets to see what happens in our third point.
The standard error increases from 1.43527 to 7.953616. Let’s calculate the standard error of the mean stderror(data) Let’s take an example the above example the first value is 5, suppose if we entered wrongly into 50. The standard error of the mean tends to decrease as the sample size grows. Check any outliers that exist in the data set.ģ. In a dataset, the bigger the standard error of the mean, the more values in the dataset are spread out around the mean.Ģ. When analyzing the standard error of the mean, keep the following three points in mind:ġ. The standard error of the mean (SEM) is a measure of how widely values are distributed around the mean. Okay, now that we have the standard error of the mean, how do we interpret it? Interpretation The standard error of the mean comes out to be 1.43527 once more. Yes, it’s ready to calculate the standard error of the mean stderror(data) Now we can use the same data set for illustration.
HOW DO I CALCULATE STANDARD ERROR HOW TO
The code below demonstrates how to do so:įirst, we need to create a standard error function stderror <- function(x) sd(x)/sqrt(length(x)) Method 2: Own FunctionĪnother option is to create your own function to determine the standard error of the mean for a dataset. It turns out that the standard error of the mean is 1.43527. Now we can calculate the standard error of the mean std.error(data) Now we can create dummy data set for the SEM calculation data <- c(5,8,9,12,13) The code below demonstrates how to use this function:įirst, we need to load plotrix library in the R console library(plotrix) The first method is to utilize the Plotrix library’s built-in std.error() function to determine the standard error of the mean. It’s worth noting that both strategies get identical outcomes.

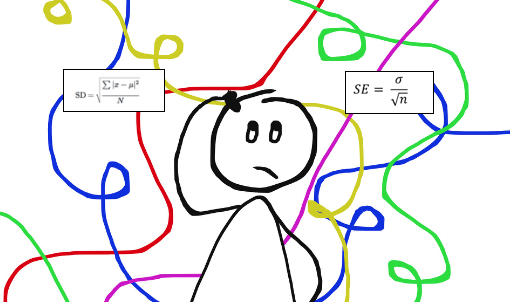
In this lesson, you’ll learn how to compute the standard error of a dataset in R using two different methods. The standard deviation is SD, and the number of observations is N. The ratio of the standard deviation to the root of the sample size is the formula for the standard error of the mean. In another way, the standard error of the mean is a metric for determining how widely values in a dataset are spread out. The standard deviation of the mean (SEM) is another name for it. Standard Error of the Mean in R, A method for calculating the standard deviation of a sampling distribution is the standard error of the mean. If you want to read the original article, go here How to Calculate the Standard Error of the Mean in R

Visit for the most up-to-date information on Data Science, employment, and tutorials finnstats.


 0 kommentar(er)
0 kommentar(er)
